In the previous article, I show results from two regression models that predict religious affiliation and degree of religiosity. I use the models to compare hypothetical respondents who are at their national means for all explanatory factors; then I vary one factor at a time, comparing someone at the 25th percentile with someone at the 75th percentile. I compute the different in the predicted probability of religious affiliation and the predicted level of religiosity:
1) In almost every country, a hypothetical respondent with high Internet use is less likely to report a religious affiliation. The median effect size across countries is 3.5 percentage points.
2) In almost every country, a hypothetical respondent with high Internet use reports a lower degree of religiosity. The median effect size is 0.36 points on a 10-point scale.
These results suggest that Internet use might cause religious disaffiliation and decreased religiosity, but they are ambiguous. It is also possible that the direction of causation is the other way; that is, that religiosity causes a decrease in Internet use. Or there might be other factors that cause both Internet use and religiosity.
I'll address the first possibility first. If religiosity causes lower Internet use, we should be able to measure that effect by flipping the models, taking religious affiliation and religiosity as explanatory variables and trying to predict Internet use.
I did that experiment and found:
1) Religious affiliation (hasrelig) has no predictive value for Internet use in most countries, and only weak predictive value in others.
2) Degree of religiosity (rlgdgr) has some predictive value for Internet use in some countries, but the effect is weaker than other explanatory variables (like age and education), and weaker than the effect of Internet use on religiosity: the median across countries is 0.19 points on a 7-point scale.
Considering the two possibilities, that Internet use causes religious disaffiliation or the other way around, these results support the first possibility, although the second might make a smaller contribution.
Although it is still possible that a third factor causes increased Internet use and decreased religious affiliation, it would have to do so in a strangely asymmetric way to account for these results. And since the model controls for age, income, education, and other media use, this hypothetical third factor would have to be uncorrelated with these controls (or only weakly correlated).
I can't think of any plausible candidates for this third factor. So I tentatively conclude that Internet use causes decreased religiosity. I present more detailed results below.
Summary of previous results
In the previous article, I computed an effect size for each factor and reported results for two models, one that predicts hasrelig (whether the respondent reports religious affiliations) and one that predicts rlgdgr (degree of religiosity on a 0-10 scale). The following two graphs summarize the results.Each figure shows the distribution of effect size across the 34 countries in the study. The first figure shows the results for the first model as a difference in percentage points; each line shows the effect size for a different explanatory variable.
The factors with the largest effect sizes are year of birth (dark green line) and Internet use (purple).
For Internet use, a respondent who is average in every way, but falls at the 75th percentile of Internet use, is typically 2-7 percentage points less likely to be affiliated than a similar respondent at the 25th percentile of Internet use. In a few countries, the effect is apparently the other way around, but in those cases the estimated effect size is not statistically significant.
Similarly, when we try to predict degree of religiosity, people who use the Internet more (again comparing the 75th and 25th percentiles) report lower religiosity, typically 0.2 to 0.7 points on a 10 point scale. Again, the effect size for Internet use is bigger than for education, income, or other media.
Of course, what I am calling an "effect size" may not be an effect in the sense of cause and effect. What I have shown so far is that Internet users tend to be less religious, even when we control for other factors. It is possible, and I think plausible, that Internet use actually causes this effect, but there are two other possible explanations for the observed statistical association:
1) Religious affiliation and religiosity might cause decreased Internet use.
2) Some other set of factors might cause both increased Internet use and decreased religiosity.
Addressing the first alternative explanation, if people who are more religious tend to use the Internet less (other things being equal), we would expect that effect to appear in a model that includes religiosity as an explanatory variable and Internet use as a dependent variable.
But it turns out that if we run these models, we find that religiosity has little power to predict levels of Internet use when we control for other factors. I present the results below; the details are in this IPython notebook.
Model 1
The first model tries to predict level of Internet use taking religious affiliation (hasrelig) as an explanatory variable, along with the same controls I used before: year of birth (linear and quadratic terms), year of interview, education, income, and consumption of other media.The following figure shows the effect size of religious affiliation on Internet use.
In most countries it is essentially zero, but in a few countries people who report a religious affiliation also report less Internet use, but always less than 0.5 points on a 7 point scale.
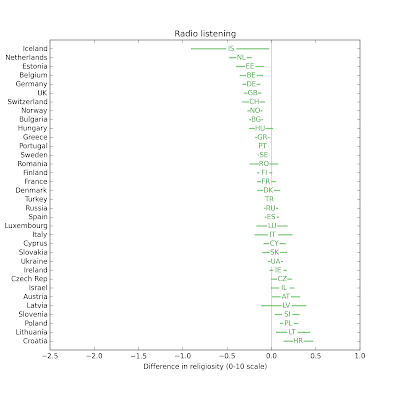
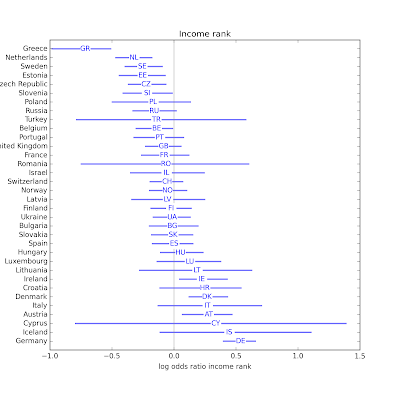
The following figure shows the distribution of effect size for the other variables on the same scale.
If we are trying to predict Internet use for a given respondent, the most useful explanatory variables, in descending order of effect size, are year of birth, education, year of interview, income, and television viewing. The effect sizes for religious affiliation, radio listening, and newspaper reading are substantially smaller.
The results of the second model are similar.
Model 2
The second model tries to predict level of Internet use taking degree of religiosity (rlgdgr) as an explanatory variable, along with the same controls I used before.The following figure shows the estimated effect size in each country, showing the difference in Internet use of two hypothetical respondents who are at their national mean for all variables except degree of religiosity, where they are at the 25th and 75th percentiles.
In most countries, the respondent reporting a higher level of religiosity also reports a lower level of Internet use, in almost all cases less than 0.5 points on a 7-point scale. Again, this effect is smaller than the apparent effect of the other explanatory variables.
Again, the variables that best predict Internet use are year of birth, education, year of interview, income, and television viewing. The apparent effect of religiosity is somewhat less than television viewing, and more than radio listening and newspaper reading.
Next steps
As I present these results, I realize that I can make them easier to interpret by expressing the effect size in standard deviations, rather than raw differences. Internet use is recorded on a 7 point scale, and religiosity on a 10 point scale, so its not obvious how to compare them.
Also, variability of Internet use and religiosity is different across countries, so standardizing will help with comparisons between countries, too.
More results in the next installment.